Отклонение это

Понятие социальной нормы и отклонений от нее

Определение 1

Социальная норма – это правила, образцы действия либо поведения людей или их группы, установленные в данном обществе.

В психологии, педагогике и социологии очень подробно рассматриваются вопросы отклоняющегося поведение, его причин и закономерностей. Для определения данной категории нарушений используются различные термины: девиантное поведение, асоциальное поведение, устойчивые отклонения в поведении личности.

Основными причинами отклоняющегося поведения исследователи называют:

трудности подросткового возраста, и самоопределения личности;
неустойчивость социального поведения в обществе;
низкая самооценка и комплекс неполноценности;
нестабильные условия развития.

Замечание 1

Следует отметить тот факт, что в реальности «чистых» отклонений не бывает. Один тип отклонения провоцирует другой, одна группа отклонений имеет свойство накладываться на другую. Можно совершенно уверенно говорить о том, что социальные отклонения обычно вызваны либо отклонениями в здоровье, либо психическими или педагогическими отклонениями.

Динамика формирования пола и отклонения от нормы

Освещается процесс формирования пола в его динамике. Анализируется воздействие основных факторов на становление пола

Большое внимание уделено тому, как между собой взаимосвязаны биологические и социальные факторы становления пола, где проходит грань между биологией и социумом. Вопрос обсуждается с разных аспектов с медицинской точки зрения, с психологической, педагогической, социальной

Акцент сделан на том, как малейшие изменения в действии того или иного фактора приводят к значительным отклонениям от нормы полоролевого поведения. Рассмотрены отклонения от нормы и факторы, под влиянием которых они формируются. Представлены принципы социализации мальчиков и девочек на разных возрастных этапах, показана разница между процессами взросления, обозначены социальные трудности становления пола.

Определение понятий «норма» и «отклонение от нормы»

Понятие нормы широко используется в различных научных сферах, таких как: психология, педагогика, медицина, социология и многие другие. В соответствии с этим невозможно дать единое определение, удовлетворяющее каждую из научных сфер и сводящее воедино все характеристики, которые подразумеваются при упоминании понятия «норма».

Сложность в определении данного понятия состоит не только в терминологии, но и в содержании, которое каждая из наук вкладывает в это понятие. Примером могут выступать нравственные номы – невозможно зафиксировать их раз и навсегда, не оставляя возможности изменять и дополнять.

Если говорить о самом обобщенном и отстраненном определении номы, то можно сказать, что норма – это какое-либо идеальное образование, условное обозначение объективной реальности, показатель, который характеризует действительность, но не существует в ней в реальном воплощении.

Антиподом нормы выступает отклонение – явление, не соответствующее представлениям об идеальном образовании, выбивающееся из представлений общества о нормальных процессах и явлениях.

Еще термины по предмету «Конфликтология»

Прием «Салями»

тактический прием на переговорах, суть которого в поэтапном разъяснении своей позиции. Применяется с целью затягивания переговоров и получения максимальной информации о партнере.

Агрессивное поведение животных

(от лат. aggressiо – нападение) – одна из основных форм поведения животных, направленных на уничтожение или устранение из сферы влияния др. живых организмов, чаще представителей того же, реже – др. вида животных. А. п. ж. слагается из двух противоположных компонентов – нападения и бегства, относительная сила и взаимодействие которых определяют интенсивность и результативность зооконфликтов между животными.

Социологический уровень

представляет собой системное исследование причин, социодинамики развертывания конфликтных взаимодействий, их типов, видов и форм проявления, способов разрешения, роли их в развитии общества, социальных групп и общностей.

Отклонение
Норма
Нормы
Вероятное отклонение (срединное отклонение)
Норма доходности (норма процента)
Отклонение по завершению
Отклонение по срокам
Отклонение по стоимости
Проектные отклонения
Срединное отклонение
Среднеквадратическое отклонение
Среднее отклонение
Отклонением расположения
Отклонением формы
Анализ отклонений
Масштаб отклонений
Отчет об отклонениях
Отклонение социальное
Действительное отклонение
Основное отклонение

Примеры применения отступления и отклонения

Отступление может использоваться для создания блока текста, который будет выходить за пределы общего текста страницы и будет иметь другой фоновый цвет или другой шрифт

Например, такой блок можно использовать для выделения основной идеи статьи или выделения важной информации

Отклонение может использоваться для создания списка. Список может быть маркированным, когда каждый элемент списка выделен символами, такими как точки, круги или номера, или нумерованным, когда каждый элемент списка имеет свой уникальный номер. Список может быть очень полезным для организации информации и обеспечения ее читаемости.

Маркированный список:
- Яблоки
- Апельсины
- Бананы
Нумерованный список:
1. Подготовить инструменты
2. Подготовить поверхность
3. Начать работу

Понятие социального выпадения

Следуя из вышесказанного можно сделать вывод о том, что любое нарушение возможностей человека затрагивает всю систему личности и приводит к так называемому «социальному выпадению». Данное явление рассматривается исследователями из различных областей знаний и каждая из них имеет свои теории «выпадений».

Например, отклонения в поведении детей, которые имеют ограниченные возможности, рассматриваются в медицинской модели выпадения. Согласно ей, имеющиеся в поведении несоответствия социальным нормам представляют собой особую патологию здоровья, причиной которой выступают эндокринные нарушения, генетические отклонения и т.д.

В конце 19 начале 20 веков на основе медицинской модели была сформирована теория социальной полезности людей с ограниченными возможностями, получившая широкое распространение во всем мире. Основная идея данной теории заключается в том, что в любом обществе есть люди, имеющие какие-либо ограничения, однако это совершенно не мешает им осуществлять элементарную социально полезную деятельность.

Таким образом, люди с ограниченными возможностями, при специальном профессиональном обучении способны сами себя обеспечивать, и не быть обузой для окружающих людей и общества в целом

И что немаловажно, это способствует их личностному развитию и самоутверждению

В середине двадцатого века медицинскую модель сменила модель социальная, толчком к развитию которой стала теория психоанализа.

Основной идеей данной модели выступила мысль о том, что отклоняющееся поведение необходимо рассматривать не только как результат отклонений в здоровье, но и как результат неправильно построенного процесса воспитания и взаимодействия с окружающим миром. В процессе разработки данной теории приоритеты в объяснении социальных выпадений претерпели значительные изменения:

неадекватное поведение стало рассматриваться как результат деформированного процесса накопления социального опыта, в результате чего происходят субъективные изменения и деформация личности;
источником социальных выпадений все чаще стали называться семейное неблагополучие, отсутствие педагогической культуры родителей, отсутствием тепла и любви со стороны родителей к ребенку.

Таким образом, постепенно накапливающиеся неразрешенные конфликты являются результатом, проявляющимся в отклоняющемся поведении.

Еще одной главной идеей социальной модели является утверждение о том, что отклоняющееся поведение поддается коррекции и возможно полное его исправление.

Основные понятия

Для объяснения термина «среднеквадратичное отклонение» необходимо ознакомиться с используемой терминологией.

Определение 1

Средним арифметическим или средней величиной называют число, являющееся суммой всех проведённых измерений, разделённой на количество этих измерений.

Для пяти чисел $a_1, a_2, a_3, a_4$ и $a_5$ средняя величина $M$ определяется по формуле

$M=\frac{a_1+ a_2+ a_3+ a_4+ a_5}{5}$.

Со средним арифметическим также связано другое понятие — математическое ожидание.

Определение 2

Математическое ожидание — это значение среднего арифметического некоторой величины при стремлении количества измерений этой величины к бесконечности.

Математическое ожидание также могут обозначать буквой $M$, а среднее арифметическое некоторого количества измерений исследуемой величины могут называть оценкой математического ожидания.

Определение 3

Абсолютной погрешностью измеряемой единичной величины, иногда также называемой вариантой, является её разность со средним значением $M$.

Для того чтобы найти абсолютную погрешность некоторого единичного измерения $x_i$, обозначаемую греческой буквой $Δ$ (произносится как «дельта»), необходимо отнять от измеренного значения $x_i$ среднее арифметическое $M$: $Δx_i=x_i – M$.

Часто для оценки единичного измерения пользуются не только абсолютной погрешностью, но и относительной погрешностью $δ$, она рассчитывается по формуле:

$δ=\frac{|Δx_i|}{M} \cdot 100$%.

Оценив относительную погрешность каждого измерения, можно отбросить значения, погрешность которых слишком большая и при дальнейших расчётах использовать только значения с небольшими относительными погрешностями.

Определение 4

Среднее арифметическое квадратов всех абсолютных погрешностей называют дисперсией и обозначают буквой $D$.

Дисперсия является характеристикой разброса значений некоторой измеряемой случайной величины $x$.

Изучаем определения

Отступление и отклонение: в чем разница?

Отступление и отклонение — два понятия, которые могут показаться похожими, но имеют существенные различия. Отступление — это изменение маршрута внутри зоны боевых действий с целью обойти препятствие или укрепление противника. Возможны как малые, так и большие отступления в зависимости от ситуации на поле боя. Отступление является планируемым действием командира и часто связано с принятием тактических решений.

Отклонение же — это непреднамеренное изменение направления движения войск в результате воздействия противника или изменения условий боевых действий. В отличие от отступления, отклонение возникает внезапно и чаще является не контролируемым командованием событием. Отклонение может приводить к значительной потере времени и сил, поэтому задачей командования является минимизировать его последствия.

Таким образом, хотя отступление и отклонение оба представляют изменения маршрута движения войск, отличия в их смысловой и технической основе являются заметными. Различие между ними также заключается в роли командования и степени их планирования. Успешное выполнение отступления и минимизация отклонения во многом зависят от подготовки войск и владения сценарием возможных событий неподконтрольной ситуации на поле боя.

Стандартное отклонение

Прежде чем мы сможем понять дисперсию, нам сначала нужно понять стандартное отклонение , обычно обозначаемое как σ .

Формула для расчета стандартного отклонения:

σ = √(Σ (x i – μ) 2 / N)

где μ — среднее значение совокупности, x i — i -й элемент совокупности, N — размер совокупности, а Σ — просто причудливый символ, означающий «сумма».

На практике вам редко придется вычислять стандартное отклонение вручную; вместо этого вы можете использовать статистическое программное обеспечение или калькулятор.

На самом базовом уровне стандартное отклонение говорит нам, насколько разбросаны значения данных в наборе данных. Чтобы проиллюстрировать это, рассмотрим следующие три набора данных вместе с соответствующими стандартными отклонениями:

стандартное отклонение = (совсем нет разброса)

стандартное отклонение = 1,63 (некоторый разброс)

стандартное отклонение = 45,28 (большой разброс)

Термин «стандартное отклонение» можно понять, взглянув на два слова, которые его составляют:

«отклонение» — это относится к расстоянию от среднего значения.
«Стандарт» — это относится к «стандартному» или «типичному» расстоянию, на котором значение находится от среднего значения.

Как только вы поймете стандартное отклонение, вам будет намного легче понять дисперсию.

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

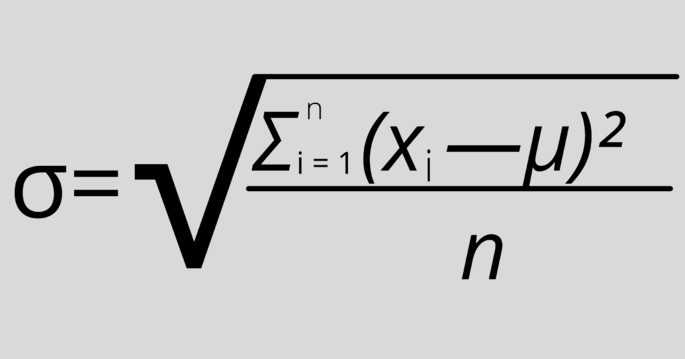Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

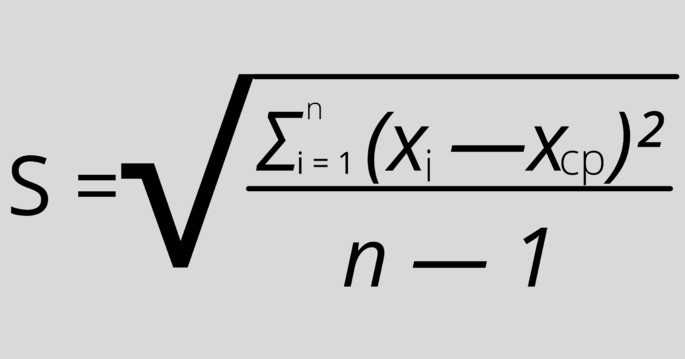Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

только её часть – используется формула S (с «n–1»),
полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

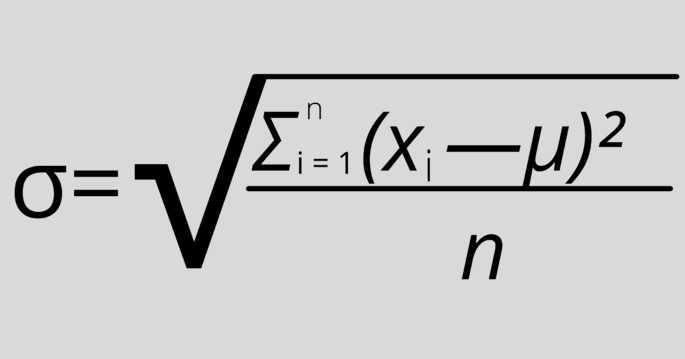
Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

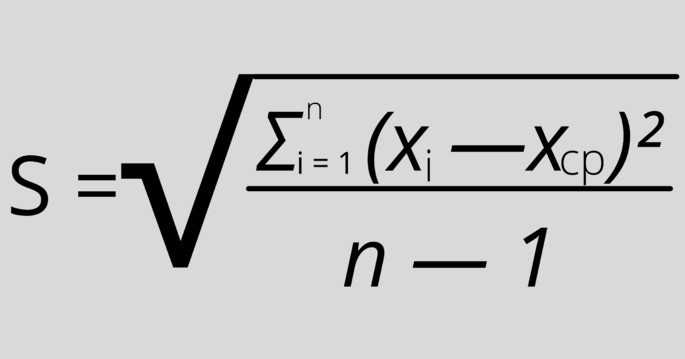
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Практические советы для определения отступления и отклонения

1. Понимание основных понятий

Перед тем, как начать определять отступление и отклонение, необходимо понимать, что подразумевается под этими терминами. Отступление — это изменение положения войск с целью занять более выгодное положение или уйти от преследования противника. Отклонение — это организованный отход войск от позиций под давлением противника с целью сохранения жизни и сохранения боеспособности.

2. Анализ обстановки и принятие решения

Для определения, какое действие в данной ситуации является более целесообразным — отступить или отклониться, необходимо проанализировать обстановку. Стоит оценить силы и возможности противника, свои силы и возможности, территорию и другие факторы, которые могут повлиять на развитие боевых действий. После анализа обстановки и принятия решения о необходимости отступления или отклонения, необходимо быстро и организованно перейти к его осуществлению.

3. Организация отступления или отклонения

Организация отступления или отклонения является ключевым моментом в ситуации, когда они необходимы. Во время отступления или отклонения необходимо организованно и сплоченно действовать, следить за безопасностью и боеспособностью своих подразделений

Важно также устанавливать соответствующие связи между подразделениями для координации действий и соблюдения единой тактики

Создайте задерживающий огневой барьер, чтобы замедлить наступление противника.
Используйте препятствия на пути противника.
Назначьте ответственных за задачи организации отступления или отклонения.

Если ситуация этого требует, можно использовать различные маневры для затруднения действий противника

При этом важно не терять боеспособность и оставаться сплоченной командой

4. Анализ результата

После завершения отступления или отклонения следует провести анализ результата. Стоит оценить, удалось ли сохранить боеспособность и жизнь подразделений, были ли достигнуты поставленные цели. Из проведенного анализа можно извлечь уроки и использовать их в будущих боевых действиях.

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

среднее квадратическое отклонение

Или стандартное отклонение. Оно обозначается греческой буквой «сигма», и коль скоро у нас выборочная совокупность, то добавляем соответствующий подстрочный индекс:

– выборочное среднее квадратическое отклонение.

Чем меньше стандартное отклонение (и дисперсия), тем меньше вариация – тем бОльшее количество вариант находится вблизи выборочной средней. Но у нас, как нетрудно «прикинуть на глазок», разброс довольно-таки велик – значительное количество вкладов расположено далековато от , и поэтому значение получилось немалым.

Следующая часть задачи состоит в том, чтобы корректно оценить генеральную дисперсию и генеральное среднее квадратическое отклонение .

В 1-й части урока я рассказал о том, что выборочная дисперсия представляет собой смещённую оценку генеральной дисперсии. Это означает, что если мы будем проводить неоднократные выборки из той же генеральной совокупности, то полученные значения будут систематически занижено оценивать

Обращаю ваше внимание, что это не значит, что будет всегда меньше, чем

И поэтому выборочную дисперсию, как намекает условие, нужно поправить: – исправленная выборочная дисперсия

и, соответственно: или 240,30 д.е. – исправленное среднее квадратическое отклонение.

и – это уже несмещённые оценки генеральной дисперсии и генерального стандартного отклонения соответственно.

Ввиду большого объёма выборки (более 100 вариант) этой поправкой можно пренебречь, но всё же мы не будем «разбрасываться» 30 «копейками».

Ответ: ; в качестве оценки соответствующих генеральных показателей принимаем и .

Рассмотренные выше показатели (размах вариации, среднее линейное отклонение, дисперсия, стандартное отклонение) входят в группу абсолютных показателей вариации, которые обладают рядом неудобств. Так, если в прорешанной задаче не уменьшать варианты в 1000 раз, то дисперсия получится в миллион раз больше! Да-да, не , а . И возникает естественное желание привести результаты к некому единому стандарту.

Для этого существуют показатели относительные, и самым известным из них является