Динамика

Масса и Вес

В системе СИ измеряется в килограммах.  Если не ищете легких путей и хотите быть особенно экстравагантным, можете измерять в фунтах, пудах и унциях.

Важно! Не стоит путать массу тела и вес. Ведь масса – скалярная величина, а вес – это сила, с которой тело действует на опору или подвес

Другими словами, масса всегда остается постоянной, это собственная характеристика тела. А вот вес может меняться. Например, Ваш лунный вес будет отличаться от земного, т.к. ускорение свободного падения на планетах различно.

Вы все еще читаете? Поздравляем, Вы просто молодцы! Давайте переходить к законам Ньютона, ведь рассматривая основы динамики невозможно обойти их стороной. Законы Ньютона — основные законы динамики.

Сила упругости. Закон Гука

Сила упругости – это сила, возникающая при деформации тела.

Деформация – это изменение формы и объема тела в результате неодинакового смещения различных его частей под действием силы.

Виды деформаций:

• упругие – это деформации, при которых после прекращения действия внешних сил тело принимает первоначальные размеры и форму (растяжение, сжатие, изгиб, кручение, сдвиг);
• пластические – это деформации, которые сохраняются в теле после прекращения действия внешних сил.

Основные величины, характеризующие деформацию

Абсолютное удлинение – изменение размеров тела под действием силы.

Обозначение – ​\( x \)​ или ​\( \Delta{l} \)​, единицы измерения – м.

где ​\( l_0 \)​ – длина тела до действия силы (начальная длина),
​\( l \)​ – длина тела во время действия силы.

Относительное удлинение – это количественная мера степени деформации тела.

Обозначение – ​\( \varepsilon \)​, единиц измерения нет.
Относительное удлинение равно отношению абсолютного удлинения к длине тела до действия силы (начальной длине тела):

Механическое напряжение – это сила, действующая на единицу площади поперечного сечения.

Обозначение – ​\( \sigma \)​, единицы измерения – Па (Паскаль):

Закон Гука
Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена в сторону, противоположную деформации:

где ​\( k \)​ – жесткость пружины.

Знак «–» в законе Гука говорит о том, что сила упругости всегда направлена противоположно смещению частиц тела при деформации. При решении задач им можно пренебречь.

Виды силы упругостиСила реакции опоры – это сила, действующая на тело со стороны опоры.
Обозначение – ​\( N \)​, единицы измерения – Н.Сила натяжения – это сила, действующая на тело со стороны подвеса.
Обозначение – ​\( T \)​, единицы измерения – Н.

Важно!
Соединения пружин:

последовательное

• параллельное

Важно!
Если тело движется по окружности и нет силы трения между соприкасающимися поверхностями, то оно вынуждено наклоняться под углом к поверхности, по которой движется, иначе его центростремительное ускорение станет равным нулю и оно поедет по касательной к окружности согласно первому закону Ньютона. Чтобы удержаться на круге (сохранить равновесие), оно наклоняется к центру

В этом случае

Если тело совершает мертвую петлю, то в верхней точке петли и сила тяжести, и сила нормального давления будут направлены вниз, поэтому

В нижней точке мертвой петли сила нормального давления направлена вверх и больше силы тяжести. В этом случае

Закон всемирного тяготения. Искусственные спутники Земли

Всякое тело, имеющее массу, является источником гравитационного поля – поля тяготения.

Закон всемирного тяготения
Два тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению масс этих тел, обратно пропорционален квадрату расстояния между ними и направлен вдоль линии, соединяющей эти тела:

где ​\( G \)​ – гравитационная постоянная.

Гравитационная постоянная численно равна силе притяжения между двумя телами массой по 1 кг, расположенными на расстоянии 1 м:

Закон справедлив для:

• материальных точек;
• однородных шаров;
• материальной точки и шара;
• концентрических тел.

Искусственный спутник Земли – это тело, которое обращается вокруг Земли.
Траектория движения искусственных спутников – эллипс, но мы для упрощения считаем, что они движутся по окружности.
Линейная скорость такого движения есть первая космическая скорость.Первая космическая скорость – это горизонтально направленная минимальная скорость, с которой тело могло бы двигаться вокруг Земли по круговой орбите, т. е. стать искусственным спутником Земли.

На рисунке ​\( R \)​ – радиус Земли, ​\( H \)​ – высота спутника над поверхностью Земли, ​\( r \)​ – высота орбиты спутника:

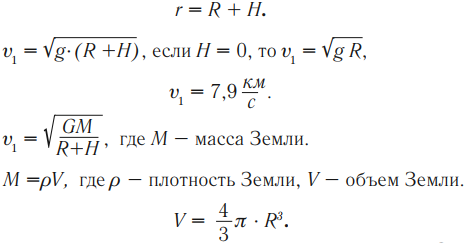
Период обращения искусственного спутника Земли можно рассчитать по формуле:

Вторая космическая скорость – это наименьшая скорость, которую надо сообщить телу, чтобы его орбита в поле тяготения Земли стала параболической, т. е. чтобы тело могло стать искусственным спутником Солнца:

Важно!
При решении задач следует помнить, что в законе всемирного тяготения расстояние берется от центра тела, а не от его поверхности

Похожие термины:

PRICE MOVEMENTSСм. ИНДЕКСЫ; ПРИНЦИП ФЛУКТУАЦИИ; СВИНГ; ЦИКЛ ДЕЛОВОЙ АКТИВНОСТИ; ЦИКЛ СПЕКУЛЯТИВНЫЙ

движение цен во внешней торговле, гарантирующее изменение цен на отдельные товары, товарные группы, экспорт и импорт в целом во внешней торговле отдельных стран и во всей международной торговле.

частота изменения ассортимента товаров с учетом сезонности, праздников, включая обновление оформления витрин, выкладки товаров.

изменение доходов от предпринимательства, коммерческой деятельности под влиянием внутренних и внешних факторов.

характер изменения экономических показателей во времени, определенный путем составления и анализа ряда таких показателей.

изменения в лесном фонде, происходящие во времени и пространстве под влиянием антропогенных и природных факторов.

изменение спроса и предложения на рынке, измеряемое с помощью соответствующих индексов.

движение конфликтного взаимодействия, стадии и фазы его развития. Пути предупреждения (предотвращения) конфликтов: предотвращение причин конфликта на различных уровнях; — поддержание сотрудниче

процесс, посредством которого взаимодействие между конкретными индивидами уменьшают напряжение каждого из них в данной ситуации и приводит их к взаимному удовлетворению. Этот процесс объясняет:

долгосрочная тенденция (от 1 до 5 лет) динамики или направление развития первичного рынка ценных бумаг.

показатели, отражающие изменение стоимости или физического объема оптовой реализации средств произ-ва во времени (темпы роста, темпы прироста). См. Индексы объема оптовой реализации средств произ

изменение затрат на единицу продукции, в том числе на производство и сбыт с течением времени в результате воздействия различных внутренних и внешних факторов.

изменение величины спроса с течением времени на товары и товарные группы. Измеряется соответствующими индексами.

метод изучения процесса развития (включая ускоряющийся или замедляющийся рост, стагнацию и возникновение кризисов, разрушающих базовые структуры) в сложных системах, основные переменные к-рых им

Метод, используемый в теории экономической динамики (dynamic economics), специфическое свойство которого состоит в том, что скорости изменения значений параметров (parameters) и равновесных значений переменны

зависимость изменения текущих затрат на производство продукции от роста или сокращения объема производства.

Период, когда цены по сделкам изменяются в узком диапазоне, показывая лишь небольшие сдвиги вверх или вниз. Синоним термина horizontal price movement (горизонтальное движение цен).

С 1960-х годов стратегический менеджмент прошёл большой путь. Поначалу исследования и практика развивались относительно медленно, в 1970-1980-х годах произошло существенное ускорение, а в 1990-х годах раз

развитие экономики на основе экономич. законов данного способа произ-ва, в ходе к-рого меняются количеств, характеристики экономич. процессов и явлений, их качеств

структура, а также развиваются п

класс математических моделей экономики, в которых основное внимание сосредоточено на закономерностях ее развития во времени, по годам

Что изучает теоретическая механика?

Движение и взаимодействие физических тел подчиняются строгим законам, по которым существует наша Вселенная. Описанию и обоснованию этих законов посвящена механика – раздел физики, позволяющий рассчитывать и предсказывать движение физических тел, исходя из их основных параметров и действующих на эти тела сил. В механике рассматриваются идеальные объекты:

• материальная точка – объект, основной характеристикой которого является масса, но размеры не учитываются;
• абсолютно твёрдое тело – заполненный веществом определённый объём, форма которого не изменяется ни при каких воздействиях, а между любыми двумя точками внутри этого объёма всегда сохраняется одно и то же расстояние;
• сплошная деформируемая среда – состояние вещества в конечном объёме либо в неограниченном пространстве, в котором расстояния между произвольно взятыми точками могут изменяться в результате внешних воздействий.

Механика рассматривает законы движения, когда с течением времени изменяется либо положение одного тела относительно другого, либо взаимное расположение частей одного тела. Время, масса и расстояние для механики являются базовыми величинами.

Инерциальные системы отсчета. Первый закон Ньютона

Инерциальные системы отсчета – это системы отсчета, относительно которых тела движутся с постоянной по модулю скоростью в отсутствие или при компенсации внешних воздействий.

Инерциальной системой отсчета является система отсчета, связанная с Землей.

Первый закон Ньютона
Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или их действие компенсируется:

Физический смысл закона:

• из всех систем отсчета первый закон выделяет только инерциальные системы отсчета;
• закон утверждает, что будет происходить с телом, если на него не действуют другие тела или действие других тел скомпенсировано.

Согласно первому закону Ньютона, когда силы, действующие на движущееся тело, уравновесят друг друга, оно станет двигаться прямолинейно и равномерно, а если оно ранее покоилось, то и останется в покое.

Следствие
Если существует хотя бы одна инерциальная система отсчета, то существует и бесконечное множество таких систем.

Важно!
Скорость движения тела постоянна, если на него не действуют другие тела или действие других тел компенсируется

В чем сила, брат?

Красота – страшная сила! А еще, конечно, сила в правде, а у кого-то в деньгах. Но мы-то знаем, что все это заблуждения и домыслы. Сила – в Ньютонах!

Сила. Измеряется в Ньютонах

Единицей измерения силы в системе СИ является Ньютон. Один Ньютон – это такая сила, которую мы можем приложить к телу массой один килограмм. При этом она изменит скорость тела на 1 м/с за одну секунду.

Бывает , что на тело действует сразу несколько сил. В принципе, в мире нет тел и предметов, на которые не действуют вообще никакие силы. Вот с утра едем мы на экзамен, и так бы нам хотелось, чтоб никакие силы нас не трогали и оставили в покое… Но нет. Притяжение давит вниз, ветер сдувает вбок, кто-то еще нагло толкает в метро. В таком случае можно все эти силы представить как одну, но оказывающую то же действие, что и все. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.

Например, на рисунке ниже равнодействующая сил равна нулю, потому как лебедь рак и щука так никуда и не сдвинули воз.

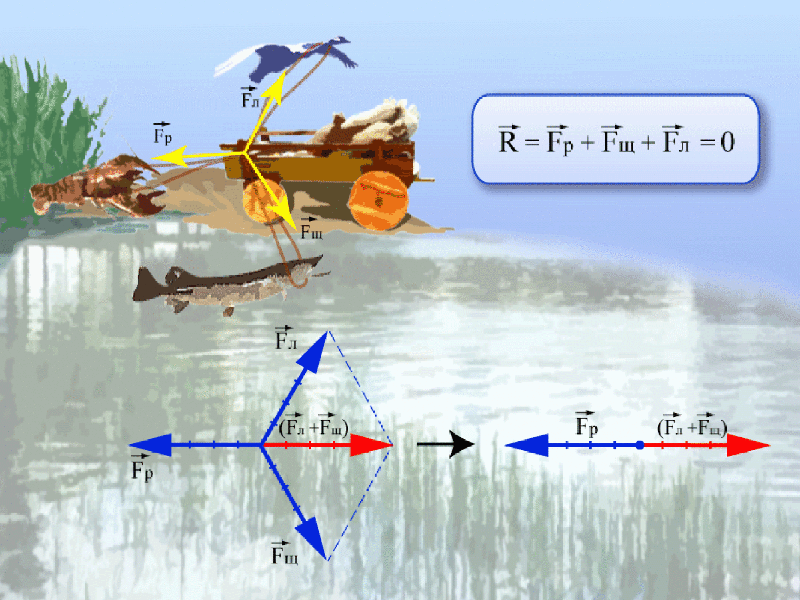Равнодействующая сила

Динамика материальной точки

Д., ос­но­ван­ная на по­ло­же­ни­ях Га­ли­лея и Нью­то­на, на­зы­ва­ет­ся клас­си­че­ской или нью­то­нов­ской. Она опи­сы­ва­ет дви­же­ние объ­ек­тов, раз­ме­ра­ми ко­то­рых мож­но пре­неб­речь (ма­те­ри­аль­ных то­чек), со ско­ро­стя­ми мно­го мень­шими ско­ро­сти све­та (дви­же­ние мик­ро­час­тиц рас­смат­ри­ва­ет­ся в кван­то­вой ме­ха­ни­ке, дви­же­ние со ско­ро­стя­ми, близ­ки­ми к ско­ро­сти све­та, – в ре­ля­ти­ви­ст­ской ме­ха­ни­ке). В клас­сич. Д. ак­сио­ма­ти­че­ски вво­дят­ся по­ня­тия не­под­виж­но­го про­стран­ст­ва и аб­со­лют­но­го вре­ме­ни, оди­на­ко­во­го во всех точ­ках про­стран­ст­ва и не за­ви­ся­ще­го от вы­бо­ра кон­крет­ной сис­те­мы ко­ор­ди­нат.

Клас­сич. Д. ба­зи­ру­ет­ся на трёх осн. за­ко­нах – Нью­то­на за­ко­нах ме­ха­ни­ки. Пер­вый из них, на­зы­вае­мый так­же за­ко­ном инер­ции, вво­дит по­ня­тие инер­ци­аль­ной сис­те­мы от­счё­та, в ко­то­рой ма­те­ри­аль­ная точ­ка по­ко­ит­ся или дви­жет­ся пря­мо­ли­ней­но и рав­но­мер­но, ес­ли на неё не дей­ст­ву­ют др. те­ла или влия­ние этих тел ском­пен­си­ро­ва­но. Ме­ру ме­ха­нич. дей­ст­вия од­но­го те­ла на дру­гое на­зы­ва­ют си­лой. Вто­рой за­кон ус­та­навли­ва­ет, что дей­ст­вие си­лы $\boldsymbol F$ на ма­те­ри­аль­ную точ­ку мас­сой $m$ вы­зы­ва­ет ус­ко­ре­ние $\boldsymbol w$ точ­ки, оп­ре­де­ляе­мое ра­вен­ст­вом $$\boldsymbol w= \boldsymbol F/m.\tag1$$Тре­тий за­кон Д. ус­та­нав­ли­ва­ет, что при взаи­мо­дей­ст­вии двух ма­те­ри­аль­ных то­чек воз­ни­ка­ет па­ра сил, рав­ных по ве­ли­чи­не и про­ти­во­по­лож­ных по на­прав­ле­нию (см. Дей­ст­вия и про­ти­во­дей­ст­вия за­кон). Ес­ли к те­лу при­ло­же­но неск. сил, то в со­от­вет­ст­вии с прин­ци­пом не­за­ви­си­мо­сти дей­ст­вия сил ка­ж­дая из них со­об­ща­ет те­лу та­кое же ус­ко­ре­ние, ка­кое она со­об­щи­ла бы, ес­ли бы дей­ст­во­ва­ла од­на. По­это­му в ка­че­ст­ве $\boldsymbol F$ в урав­не­нии $(1)$ рас­смат­ри­ва­ет­ся рав­но­дей­ст­вую­щая сил, дей­ст­вую­щих на те­ло. 

Д. ре­ша­ет 2 клас­са за­дач: пря­мые и об­рат­ные. Пря­мая за­да­ча Д. со­сто­ит в оп­ре­де­ле­нии дви­же­ния точ­ки, про­ис­хо­дя­ще­го под дей­ст­ви­ем за­дан­ных сил. Си­ла $\boldsymbol F$ счи­та­ет­ся за­дан­ной, ес­ли из­вест­на её за­ви­си­мость от вре­ме­ни $t$ и век­то­ров $\boldsymbol r$ и $\boldsymbol v$, оп­ре­де­ляю­щих по­ло­же­ние и ско­рость ма­те­ри­аль­ной точ­ки: $$\boldsymbol F=\boldsymbol F (\boldsymbol r, \boldsymbol v, t).\tag2$$В этом слу­чае ра­вен­ст­во $(1)$ пре­вра­ща­ет­ся в диф­фе­рен­ци­аль­ное урав­не­ние дви­же­ния точ­ки. Его ре­ше­ние опи­сы­ва­ет за­ви­си­мость век­то­ра $\boldsymbol r$ от вре­ме­ни и на­чаль­ных ус­ло­вий: $$\boldsymbol r= \boldsymbol r(t, \boldsymbol r_0, \boldsymbol v_0).\tag3$$

При­ме­ром по­доб­ной за­да­чи мо­жет слу­жить за­да­ча по оп­ре­де­ле­нию тра­ек­то­рии дви­же­ния сна­ря­да по его на­чаль­ной ско­ро­сти (си­лы тя­же­сти и со­про­тив­ле­ния воз­ду­ха счи­та­ют­ся из­вест­ны­ми).

Об­рат­ная за­да­ча Д. со­сто­ит в оп­ре­де­ле­нии си­лы, обес­пе­чи­ваю­щей за­дан­ное дви­же­ние: по се­мей­ст­ву за­ко­нов дви­же­ния, опи­сы­вае­мых вы­ра­же­ни­ем $(3)$, тре­бу­ет­ся вос­ста­но­вить за­ви­си­мость си­лы $(2)$ от пе­ре­чис­лен­ных ар­гу­мен­тов. Клас­сич. при­ме­ром ре­ше­ния этой за­да­чи яв­ля­ет­ся от­кры­тие И. Нью­то­ном за­ко­на все­мир­но­го тя­го­те­ния. Рас­смат­ри­вая Ке­п­ле­ра за­ко­ны дви­же­ния пла­нет, Нью­тон при­шёл к вы­во­ду, что эти дви­же­ния про­ис­хо­дят под дей­ст­ви­ем си­лы, об­рат­но про­пор­цио­наль­ной квад­ра­ту рас­стоя­ния от Солн­ца до пла­не­ты и не за­ви­ся­щей ни от вре­ме­ни, ни от ско­ро­стей дви­же­ния пла­нет.

В ря­де за­дач Д. удоб­но ис­поль­зо­вать разл. ди­на­мич. ме­ры дви­же­ния точ­ки: им­пульс (ко­ли­че­ст­во дви­же­ния) $\boldsymbol K=m \boldsymbol v$, мо­мент им­пуль­са (ки­не­ти­че­ский мо­мент) от­но­си­тель­но на­ча­ла ко­ор­ди­нат $\boldsymbol G= \boldsymbol r \times m\boldsymbol v$, ки­не­ти­че­скую энер­гию $T=mv^2/2$. При по­мо­щи этих мер урав­нение $(1)$ мож­но за­пи­сать в ви­де за­ко­на из­ме­не­ния им­пуль­са $d \boldsymbol K/dt= \boldsymbol F$, или за­ко­на из­ме­не­ния мо­мен­та им­пуль­са $d \boldsymbol G/dt= \boldsymbol r \times \boldsymbol F= \boldsymbol M$, где $\boldsymbol M$ – мо­мент си­лы от­но­си­тель­но на­ча­ла ко­ор­ди­нат, или за­ко­на из­ме­не­ния энер­гии $dT/dt=Fv=N$, где $N$ – мощ­ность си­лы $\boldsymbol F$.

Динамика

Ещё один раздел механики, который рассматривает причины, порождающие механическое движение тел, называется динамикой. Это наименование образовано от греческого слова «δύναμις», означающего силу. Основными понятиями динамики являются масса тела, сила, которая на него воздействует, энергия, импульс и момент импульса. Основными задачами – определение силы, действующей на физическое тело, по характеру его движения, и определение характера движения, исходя из заданных сил воздействия.

Значительный вклад в развитие динамики внёс британский учёный Исаак Ньютон, сформулировавший три своих знаменитых закона, которые описывают взаимодействия сил, и фактически ставший родоначальником классической динамики. Эта дисциплина изучает закономерности движения при скоростях, ограниченных интервалом от долей одного миллиметра в секунду до десятков километров в секунду. Однако при рассмотрении движения сверхмалых объектов (элементарных частиц) и сверхвысоких скоростей, приближающихся к скорости света, законы классической динамики перестают действовать.

Динамика относительного движения

Мн. за­да­чи ме­ха­ни­ки сво­дят­ся к изу­че­нию дви­же­ния од­но­го объ­ек­та от­но­си­тель­но дру­го­го, с ко­то­рым нель­зя свя­зать инер­ци­аль­ную сис­те­му ко­ор­ди­нат (напр., дви­же­ние те­ла от­но­си­тель­но вра­щаю­щей­ся Зем­ли). В этом слу­чае урав­не­ние от­но­сит. дви­же­ния ма­те­ри­аль­ной точ­ки мож­но све­сти к ви­ду $(1)$, ес­ли к чис­лу сил $\boldsymbol F$ до­ба­вить си­лы инер­ции: пе­ре­нос­ную $\boldsymbol F_e=-m \boldsymbol w_e$ и ко­рио­ли­со­ву $\boldsymbol F_c=-m \boldsymbol w_c$, где $\boldsymbol w_e$, $\boldsymbol w_c$ – со­от­вет­ст­вен­но пе­ре­нос­ное и ко­рио­ли­со­во ус­ко­ре­ния. При­ме­ра­ми за­дач Д. от­но­сит. дви­же­ния мо­гут слу­жить за­да­чи экс­пе­рим. до­ка­за­тель­ст­ва вра­ще­ния Зем­ли (па­де­ние те­ла на вра­щаю­щей­ся Зем­ле с от­кло­не­ни­ем к вос­то­ку, ма­ят­ник Фу­ко), за­да­чи опи­са­ния дви­же­ния кос­мо­нав­та от­но­си­тель­но кос­мич. стан­ции и др. На эф­фек­тах от­но­сит. дви­же­ния ос­но­ван пред­ло­жен­ный Дж. Уат­том цен­тро­беж­ный ре­гу­ля­тор уг­ло­вой ско­ро­сти вра­ще­ния, ис­поль­зуе­мый в тех­ни­ке.

Динамика, законы и формулы

Масса в динамике может рассматриваться как мера инертности тела, то есть его способности сохранять скорость неизменной до тех пор, пока на него не действуют другие тела. Всякое тело сохраняет своё первоначальное состояние относительно инерциальной системы отсчёта (т.е относительно покоя или равномерного прямолинейного движения) до тех пор, пока на него не подействуют другие тела. Система отсчёта, связанная с покоящимся или прямолинейно и равномерно движущимся телом, называется инерциальной. Также инерциальные системы отсчёта — это такие системы отсчёта, в которых выполняется закон инерции. Второй закон Ньютона. произведение массы тела на ускорение равно действующей на это тело силе, создающей это ускорение. Векторы силы и ускорения всегда имеют одинаковые направления. Второй закон Ньютона справедлив только в инерциальных системах. Ускорение, сообщаемое телу в результате одновременного действия нескольких сил, равно ускорению, которое сообщает ему их равнодействующая: Силы, с которыми два взаимодействующих тела действуют друг на друга, направлены по одной прямой, равны по модулю и противоположны по направлению: Сила, с которой связь действует на тело при его движении по окружности, направленная к центру вращения, называется центростремительной силой: Закон Гука. Абсолютное удлинение Δl стержня при упругой деформации прямо пропорционально приложенной силе: Fупр — сила упругости, k — жёсткость материала стержня. Силой упругости называют силу, возникающую в деформируемом теле. Она пропорциональна абсолютной величине деформации и направлена противоположно деформируемой силе. Все инерциальные системы отсчёта равноправны, поэтому законы механики записываются в них одинаково. В них неизменны время, масса тела, ускорение и сила. Траектория и скорость перемещения в различных инерциальных системах различны. Два тела притягиваются друг к другу по соединяющей их прямой с силой, прямо пропорциональной массам тел и обратно пропорциональной квадрату расстояния между ними: G — гравитационная постоянная (фундаментальная физическая постоянная); G = 6,67·10 -11 Н·м2/кг2. Массу можно определить как скалярную величину, характеризующую одновременно как инертные, так и гравитационные свойства тел и являющуюся мерой обоих этих свойств. Силу P, с которой тело вследствие его притяжения к Земле действует на горизонтальную опору или подвес, препятствующие его свободному падению, называют весом. Вес — сила, приложенная к опоре, а не к телу: — масса тела, g — ускорение свободного падения. Единица веса — 1 Н. Минимальная скорость υ1, которую нужно сообщить телу, чтобы ввести его на кмуговую орбиту вокруг Земли: RЗ — радиус Земли. Минисальная скорость υ2, которую нужно сообщить телу, чтобы вывести его из сферы притяжения Земли: Сила трения. Сила, которая возникает на поверхности двух соприкасающихся тел, если они перемещаются друг относительно друга, называется силой трения. Сила трения, проявляющаяся при отсутствии относительного движения тел, называется силой трения покоя: μ — коэффициент трения, зависящий от материалов и состояний трущихся поверхностей, а также от видов движения (скольжение, качение, покой и т.п.), N — сила нормального давления. Сила сопротивления среды. Для малых скоростей: Для больших скоростей: υ — скорость движения, k — коэффициент сопротивления среды, зависящий от её свойств, а также формы, размеров и состояния поверхности движущегося тела.

Сила трения

Сила трения – это сила, возникающая при движении тел или при попытке сдвинуть их с места вследствие неровностей поверхностей соприкасающихся тел.

Сила трения действует на поверхности тел и затрудняет их перемещение относительно друг друга.
Сила трения всегда направлена противоположно относительному перемещению тела, т. е. против направления вектора скорости.

Виды трения

Внешнее трение (сухое) – это трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении.

Сила трения покоя – это сила, которая возникает между соприкасающимися и покоящимися относительно друг друга поверхностями, а также при попытке сдвинуть тело с места.

Сила трения покоя саморегулирующаяся, т. е. в зависимости от внешних воздействий она может меняться от 0 до максимального значения.

где ​\( \mu \)​ – коэффициент трения, ​\( N \)​ – сила реакции опоры.

Если в условии задачи не говорится, что сила трения покоя максимальна, то ее надо находить через другие силы по второму закону Ньютона.

Cила трения скольжения – это сила, которая возникает между соприкасающимися и движущимися относительно друг друга телами.

Сила трения качения – это сила, которая возникает между соприкасающимися и катящимися относительно друг друга телами.

Внутреннее трение (жидкое или вязкое) – между слоями жидкости или газа, скорости которых меняются от одного слоя к другому.

Если движение происходит по гладкой поверхности, то сила трения равна нулю.

Способы уменьшения трения:

• выравнивание соприкасающихся поверхностей;
• смазка;
• установка шариковых и роликовых подшипников.

Важно!
Сила трения не зависит от площади соприкосновения трущихся поверхностей. Она зависит от относительной скорости тел

В этом ее главное отличие от сил тяготения и упругости, зависящих только от координат.

Важно!
Если тело удерживается на горизонтальном вращающемся диске силой трения, то