Основные величины и их формулы
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметр
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
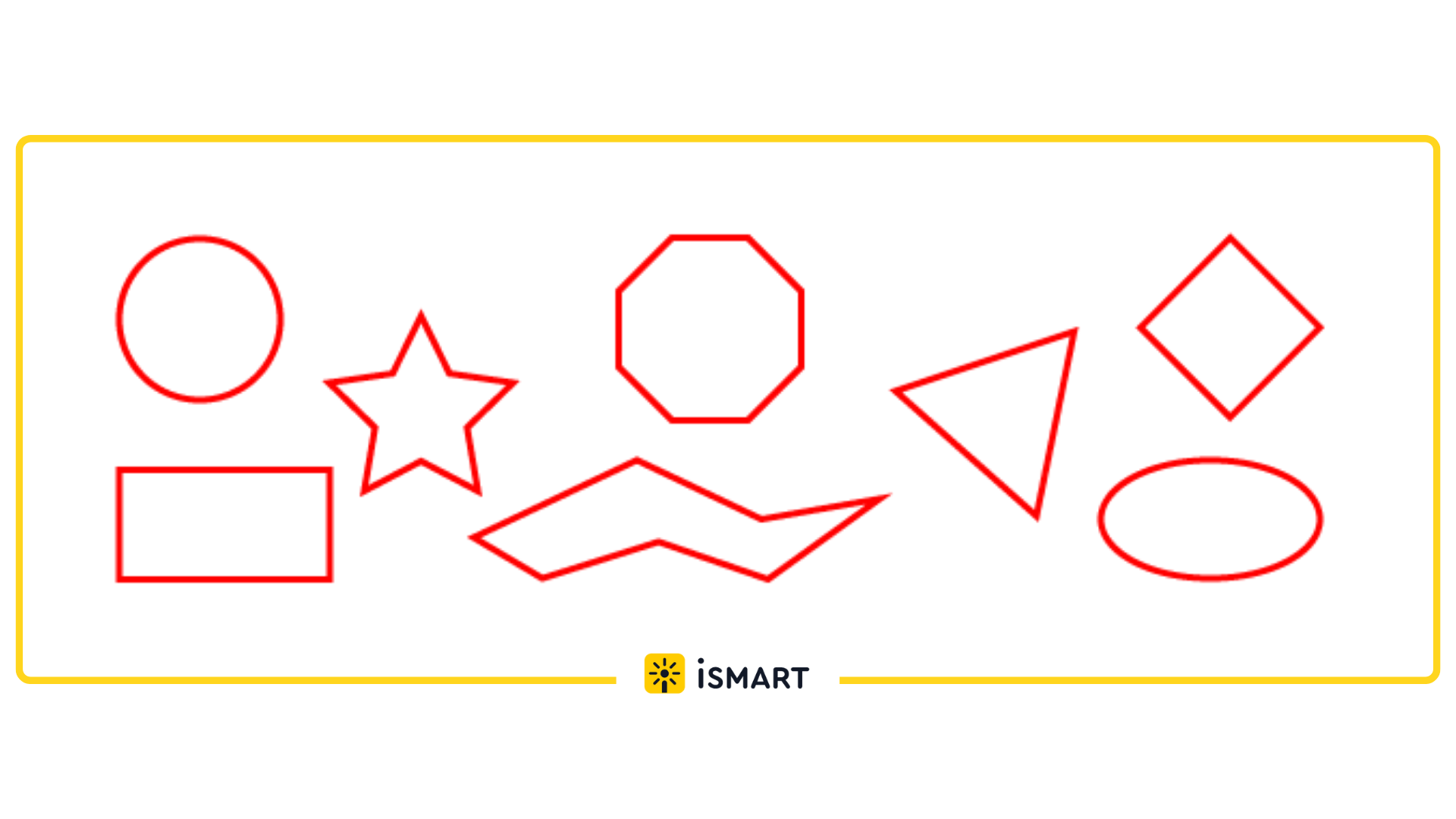
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
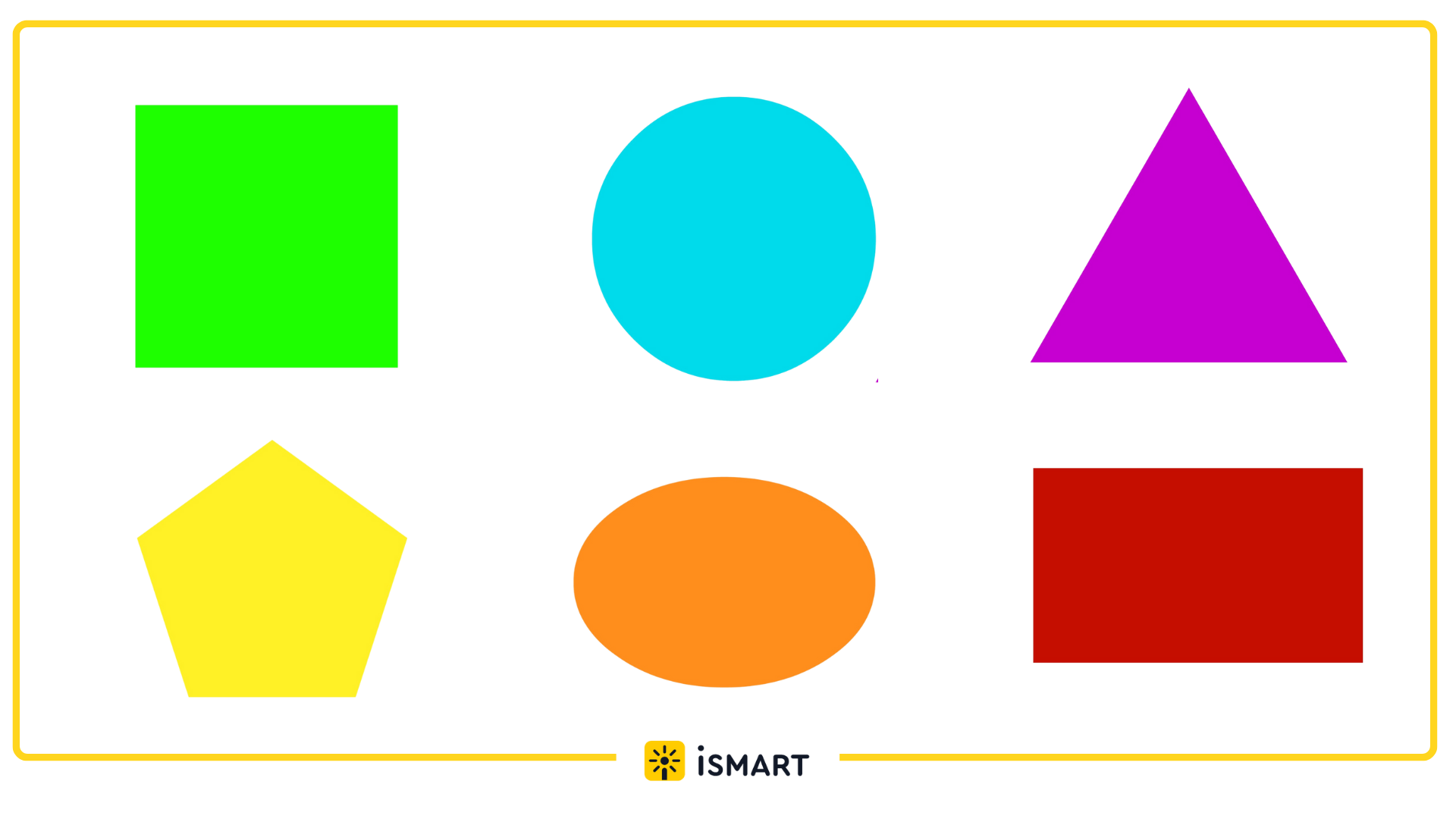
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.
Вычисление периметра и площади
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
- Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
- Параллелограмм: площадь = основание * высота
- Квадрат: площадь = сторона 1 * сторона 2
- Треугольник: площадь = ½ * основание * высота
- Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).
Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
- интерактивные задания больше похожи на игру;
- их можно отрабатывать многократно и они не будут повторяться;
- платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
- достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.
Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.
Что такое круг?
Круг – это область внутри окружности, учитывающая саму окружность.
Точка О называется центром круга.
Если центр окружности соединить отрезком с точкой окружности, то получим радиус. Радиус принято обозначать буквой латиницы–R.
Рассмотрим на примере что такое радиус: отрезок ОВ соединяет центр окружности и точку, лежащую на окружности, поэтому онявляется радиусом. ОВ=R.
Протяженность от центра до любой точки окружности одинакова, все радиусы одной окружности равны. ОС=ОВ=R.
Если отрезком, проведенным через центр окружности соединить две точки окружности, то получим диаметр окружности.
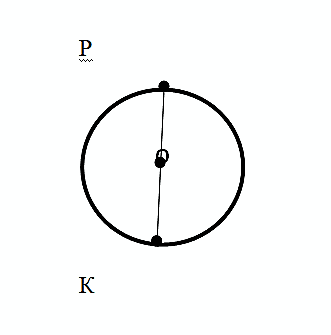
Диаметр окружности – это длина отрезка РК, диаметр обозначается буквой латиницы – D. Значит, РК= D.
На рисунке видно, что диаметр состоит из двух радиусов, то есть D=R+R=2R.
И последнее, часть окружности между любыми точками окружности, называется дугой окружности.
Основные геометрические фигуры
Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.
Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.
А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.
Разберём плоские фигуры.
Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.
Есть три вида треугольников:
- Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
- Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
- Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.
Треугольники имеют следующие свойства:
- в треугольнике напротив большего угла лежит большая сторона и наоборот;
- сумма углов треугольника всегда равна 180 градусам;
- все углы равностороннего треугольника равны 60 градусам;
- в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).
Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.
Примеры треугольников:
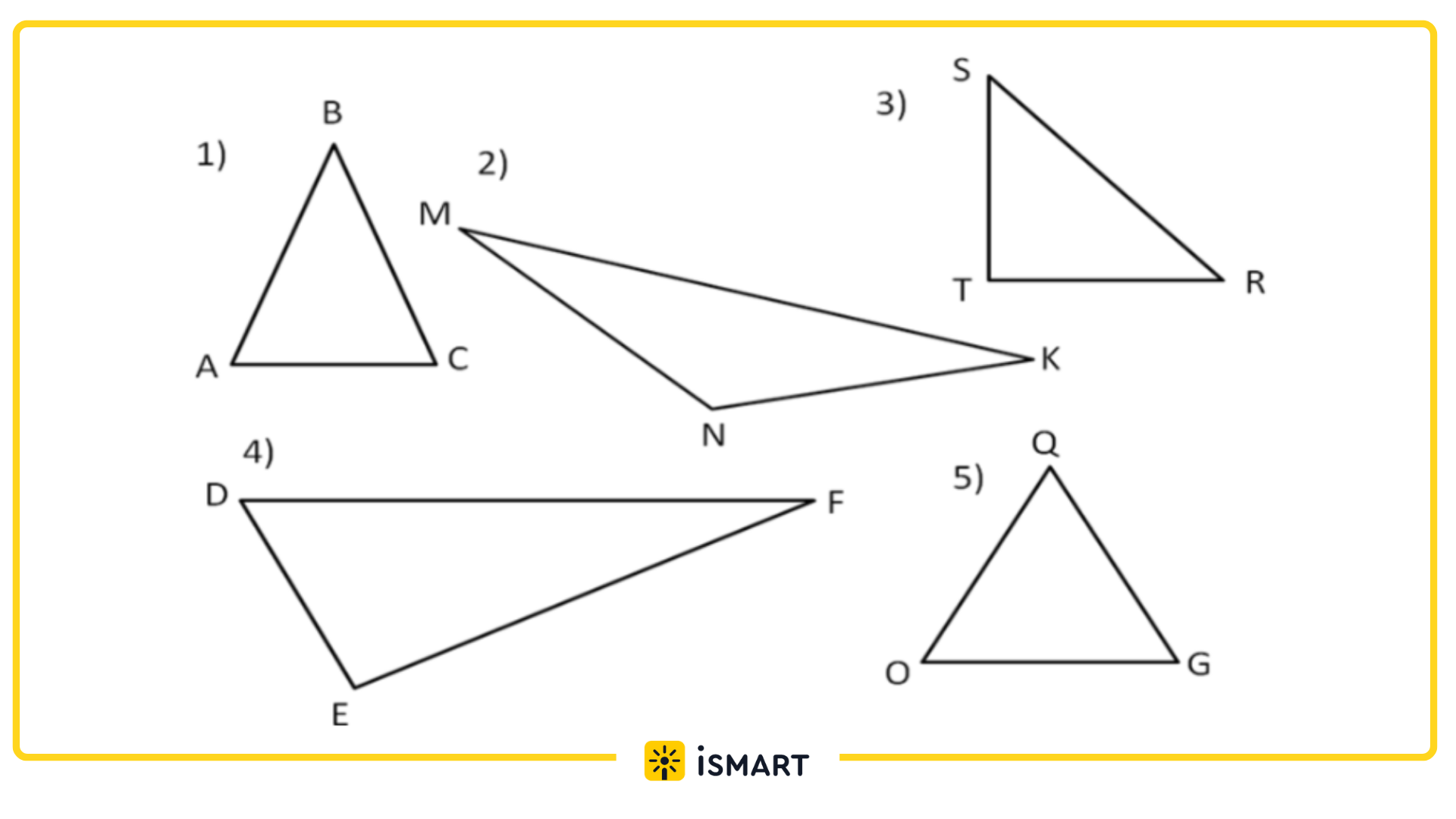
Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.
Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.
Прямоугольник

Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:
- противоположные стороны равны между собой;
- диагонали равны и делятся в точке пересечения пополам;
- около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.
Квадрат

Квадрат — это тот же прямоугольник, у которого:
- все стороны равны;
- все углы равны и составляют 90 градусов;
- диагонали равны и перпендикулярны;
- центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.
Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.
Параллелограмм имеет следующие свойства:
- противоположные стороны и углы равны;
- сумма двух любых соседних углов равна 180 градусам;
- диагонали пересекаются и точкой пересечения делятся пополам;
- каждая диагональ делит фигуру на два равных треугольника.
Что такое точка?
Как только маленький ребенок берет в ручки карандаш, он уже замечательно умеет рисовать геометрическую фигуру. Какую? – удивитесь вы. Это точка.
Точка – наименьшая, простейшая фигура геометрии, никак не измеряется.
И строить её умеет даже маленький ребенок.
Обозначать точки в математике, принято большими буквами латиницы.
Произносится:точка А, точка В, точка С.
Следующее понятие, которое мы рассмотрим, знакомо каждому с самого детства. Нет ничего проще, чем нарисовать прямую линию. Многие успешно рисовали их на новых обоях, мебели. А оказывается – она одна из основных фигур геометрии.
Интересные факты
• А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
• Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
• «Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
• «Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
• А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
• А вот одна из известных картин, созданная еще в начале прошлого века Малевичем, прославляет такую геометрическую фигуру, как квадрат. Черный квадрат на белом фоне является мистической загадкой для окружающих, притягивая к себе исследователей и восхищенные взгляды живописцев.
ПредметиМатематикаМатематика 7 класс
В словаре Даля
ж. лат. наружный очерк предмета, внешнее очертанье, вид,
образ, стать. Фигура стали осьмиугольная. Фигура мониторов походит на
огромную черепаху. Это что за фигура? что за человек. | Изображенье,
очерк вещи, подобие. Облака принимают иногда фигуру людей и животных.
Восковые фигуры, куклы. Фигуры, в живописи, ваянии: люди. | Украсы,
украшенья, узоры и разводы. Окна снаружи украшены лепными фигурками. |
Фигура риторическая, украшенье речи, оборот инословный, иносказанье,
иноречие, окольная речь, обиняк, притча. | Фигура геометрическая, очерк
площади или тело, ограниченное плоскостями, чертеж. | В картах: туз,
король, краля (дама) и хлап (валет). | В плясках: условное и совместное
движенье двух или более участников. | Фигура, волжск. фигуристый пряник,
с коим ходят в прощеный день на поклон к крестной матери. Фигурная
резьба, узорочная. Фигурность, качество по прилаг. И дурень, да фигурен.
Хоть дурень (дурен), да фигурен: в потемках хорош. Фигурчатый забор,
палисадник, узорчатый, разукрашенный. Фигуристый слог, исполненный
иноречий, намеков, окольный, темный, напыщенный. Фигуральное реченье,
окольное или иносказательное, инословное, иноречивое; обиняк.
Фигурность, свойство по прилаг. Фигурить, хитрить, лукавить; подыматься
на хитрости, на выдумки, мудрить. Фигурант, фигурантка, в балетах,
плясуны последнего разряда, для полноты и обстановки прочих.
В словаре Синонимы 4
абракадабра, анадисплосис, антанакласис, антиметабола, асиндетон, бочка, валет, вид, вираж, гипербатон, градация, дама, изваяние, изображение, изоколон, иммельман, кабриоль, квартоль, колено, комплекция, конфигурация, конь, королева, король, крест, ладья, лицо, лутц, манекен, многоугольник, оборот, образ, особа, очертания, персона, пирамида, пируэт, пневмофигура, позиция, полиграмма, положение, прием, пролепсис, птица, ранверсман, рисунок, сложение, слон, статуя, субъект, телосложение, тип, треугольник, туз, ферзь, фигурка, форма, человек, шассе, шишка, шпагат, штопор, эпистрофа
Понятие геометрической фигуры
Геометрическая фигура — это замкнутый объект в двухмерном пространстве. Она описывается различными геометрическими свойствами, такими как форма, размеры, углы и стороны. Существует множество различных геометрических фигур, каждая из которых имеет свои особенности.
Одной из самых известных геометрических фигур является параллелограмм. Он обладает четырьмя сторонами, противоположные стороны параллельны, а противоположные углы равны. Квадрат — это особый вид параллелограмма, у него все стороны и углы равны. Ромб — также параллелограмм, но у него все стороны равны, а углы необязательно прямые.
Другой важной геометрической фигурой является трапеция. У нее две параллельные стороны, называемые основаниями, и две непараллельные стороны, называемые боковыми сторонами
Эллипс — это закрытая кривая, которая представляет собой овал. У него нет сторон и углов, но есть радиусы, фокусы и оси.
Пятиугольник — это геометрическая фигура с пятью сторонами и пятью углами. У него может быть разный вид, например, правильный пятиугольник имеет все стороны и углы равными. Круг — это геометрическая фигура, образованная всеми точками, находящимися на одинаковом расстоянии от центра. Круг не имеет сторон и углов, но он имеет радиус и диаметр.
И наконец, прямоугольник — это параллелограмм, у которого все углы прямые. У него две пары противоположных равных сторон. Прямоугольник является основой для многих других геометрических фигур, таких как квадрат и параллелограмм.
Определение
Геометрические фигуры – это объекты, обладающие определенной формой и свойствами, изучаемые в геометрии. Существует множество различных геометрических фигур, каждая из которых имеет свое определение и характеристики.
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Внутренние углы параллелограмма прямые.
Круг – это фигура, представляющая собой множество точек, равноудаленных от одной оси. В круге имеется одно центральное место, называемое центром круга, и радиус – расстояние от центра круга до любой точки на его окружности.
Прямоугольник – это четырехугольник, у которого все углы прямые. Прямоугольник имеет две пары противоположных сторон, которые равны по длине, и четыре прямых угла.
Квадрат – это четырехугольник, у которого все стороны равны между собой и все углы прямые. Квадрат является специальным случаем прямоугольника.
Ромб – это четырехугольник, у которого все стороны равны между собой, а углы неравны 90 градусам. Внутренние углы ромба равны между собой.
Трапеция – это четырехугольник, у которого две параллельные стороны. Одна пара сторон называется основаниями, а другая — боковыми сторонами. Неосновательные углы трапеции могут быть как прямыми, так и тупыми.
Эллипс – это геометрическая фигура, образованная множеством точек, для которых сумма расстояний до двух данных точек постоянна. Центр эллипса – это точка, являющаяся серединой отрезка между двумя фокусами.
Треугольник – это многоугольник, образованный тремя сторонами. Внутренние углы треугольника всегда в сумме равны 180 градусам. В зависимости от длин сторон и величины углов, треугольники могут быть равнобедренными, равносторонними или разносторонними.
Основные свойства геометрических фигур
Геометрические фигуры — это объекты, которые имеют определенную форму и характеризуются определенными свойствами. Они играют важную роль в математике и имеют множество применений в различных областях науки и техники.
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны. Прямоугольник — это параллелограмм со всеми углами прямыми. Ромб — это параллелограмм, у которого все стороны равны. Квадрат — это ромб с прямыми углами, у которого все стороны равны.
Треугольник — это фигура с тремя сторонами. Он может быть разносторонним, когда все его стороны разные, равнобедренным, когда две стороны равны, или равносторонним, когда все стороны равны. Пятиугольник — это фигура с пятью сторонами. У него может быть различное количество и типов углов.
Эллипс — это геометрическая фигура, которая представляет собой замкнутую кривую. Он имеет две оси — большую и малую, и симметричен относительно центра. Круг — это частный случай эллипса, у которого все стороны и углы равны.
Эти геометрические фигуры имеют множество свойств, которые определяют их форму и характеристики. Изучение и понимание этих свойств позволяет нам анализировать и работать с различными геометрическими объектами, а также применять их в реальных задачах и решениях.
Что такое отрезок?
Давайте схематично изобразим удава. Сначала отметим две точки – голова и хвост (начало и конец). После соединим эти точки.

Получается, что схематично изображая удава, начертили еще одну геометрическую фигуру, которая называется отрезком. Давайте сформулируем определение:
Отрезок–это фигура на прямой, ограниченная двумя точками. Точки называются концами отрезка и обозначаются заглавными буквами латиницы.

Произносится: отрезок ТМ.
Если при наложении концы отрезков совпадают, то такие отрезки называют равными.
Значит, АВ=КМ
А что такое единичный отрезок, где используется?
Давайте вернемся к мультфильму. Вспомните момент, когда удава очень волновал его рост (длина). Друзья не растерялись, нашли способ его измерять. Сначала его измеряли обезьянками, потом слонами, наконец, попугаями.

Но каждый раз длина удава была разной только потому, что друзья очень отличались своими размерами. При измерении длины удава, каждый друг выступил в роли единичного отрезка, величины, в которой измерялся предмет (в слонах, обезьянах, попугаях). Так как попугай имел самый маленький размер, то длина удава в попугаях оказалась самой большой – 38 попугаев. Сформулируем определение:
Единичный отрезок – выбранная единица для измерения чего-либо.
Возьмем линейку длиной 20 см. На ней можно увидеть штрихи, делящие линейку на одинаковые кусочки, которые называют делениями. Из них состоит шкала. За единицу измерения принят отрезок длиной 1 см (единичный), и таких единиц измерения на линейке 20 штук.

Для изучения следующего понятия необходимо схематически начертить линейку. Для этого чертим луч, указываем направление луча стрелочкой, наносимделения:

Точка В, с соответствующимчисловым значением 0. Следующая точка С, с числовым значением 1. Получается, отрезок ВС считается единичным, его длина принимается за единицу измерения. Все имеющиеся точки расположены на расстоянии единичного отрезка.
Луч с нанесенным единичным отрезком, направлением, называют координатным лучом, координатной прямой.
Каждая точка на координатном луче имеет соответствующее числовое значение – координату точки.
Точке Р соответствует числовое значение 5.
Обозначается на письме: Р (5).
Произносится: координата точки Р – 5
Постарайтесь запомнить эти понятия, чтобы избежать трудностей с определением координат точек!
Фигура, которую мы рассмотрим, состоит из точки, лучей.
Давайте отметим начало двух лучей точкой.
Полученная фигура называется углом.
Угол– геометрическая фигура, состоящая из точки и выходящих из неё лучей.
В словаре Д.Н. Ушакова
ФИГУ́РА, фигуры, ·жен. (·лат. figura — вид).1. Внешнее очертание, вид, форма чего-нибудь (·устар. ). Фигура земли (мат., астр.).2. В геометрии — часть плоскости, ограниченная замкнутой ломанной или кривой линией, а также вообще совокупность определенно расположенных точек, линий, поверхностей и тел (мат.). Геометрические фигуры (напр. треугольник, параллелограмм, конус и т.д.).| В книгах — название чертежа, схемы, рисунка (обычно пишется под изображением сокращенно: фиг.; ·тип. ).3. Положение, позиция, принимаемая кем-чем-нибудь при исполнении чего-нибудь в движении (в танце, фехтовании, катании на коньках, полете в воздухе и т.д.). Первая фигура кадрили. Фигуры высшего пилотажа.4. Оборот речи, стилистический прием, усиливающий выразительность речи (лит.). Риторические фигуры. Фигура умолчания.5. Скульптурное изображение человека или животного. Восковые фигуры. Лепные фигуры на фасаде здания.| В живописи — изображение человека или животного (живоп.).6. Телосложение, внешнее очертание, формы человека. «У нее стройная, удивительной силы и ловкости фигура.» Лесков. Нескладная фигура. Статная фигура. Крупная фигура.7. перен. человек (обычно о незнакомом, неизвестном). «Мне сдается: стоит возле моей кровати та неподвижная фигура.» А.Тургенев. Подозрительная фигура.| человек, как носитель каких-нибудь социальных или индивидуальных признаков и свойств. «Велика фигура — человек с сильными чувствами, с огромными страстями?» Гончаров. «…Середняк является у нас центральной фигурой земледелия.» Сталин
Крупная политическая фигура.| Важное, значительное лицо, персона (·разг. ирон.)
В свое время он был фигурой.8. В игральных картах — название старших карт (валет, дама, король, туз).| В шахматах — название старших шашек (король, ферзь, слон, конь, ладья), в отличие от пешек.Generated by n-Cyclop






























