Специальные модуляции
Модуляции с расширенным спектром
К ним относятся различные типы модуляции с расширенным спектром, такие как расширенный спектр со скачкообразной перестройкой частоты (FHSS) и расширенный спектр прямой последовательности (DSSS). Эти модуляции являются основой методов мультиплексирования с кодовым разделением каналов и значительно расширяют спектр передачи по сравнению со спектром полезных данных. Прием посредством корреляции характеризуется специальными кодовыми последовательностями, которые в большинстве своем обладают свойствами, близкими к случайности, и которые отличают отдельные каналы друг от друга.
Это означает, что также возможны передачи, сигнал передачи которых ниже уровня фонового шума , так что существование передачи невозможно даже распознать. Как и в случае со всеми другими модуляциями, при необходимости передача сообщения может быть зашифрована. Обнаружение того, происходит ли передача, возможно только в том случае, если известны соответствующие кодовые последовательности с расширенным спектром, и посредством корреляции . Таким образом, эти методы применяются в основном в военном секторе для передачи сообщений или в области шпионажа для устройств подслушивания , которые очень трудно обнаружить . В последние годы эти методы также использовались в гражданских областях, таких как навигационные системы GPS или Galileo и в мобильной связи третьего поколения с использованием CDMA и в приложениях для стеганографии , чтобы иметь возможность обнаруживать нарушения авторских прав с использованием электронных водяных знаков, например, в музыкальных или видеофильмах.
Импульсные модуляции
С помощью этих модуляций непрерывный аналоговый сигнал преобразуется в дискретную по времени последовательность сигналов, состоящую из отдельных импульсов, которые, как и в случаях с широтно-импульсной модуляцией (ШИМ), амплитудно-импульсной модуляцией (PAM), частотно-импульсной модуляцией (PFM) и импульсной фазовой модуляцией (PPM), являются непрерывными по амплитуде. Существуют также амплитудно-дискретные версии этих методов, с PAM версия с дискретными значениями тогда называется импульсной кодовой модуляцией (PCM). ШИМ происходит как дискретно, так и непрерывно. ШИМ — приложения, например, регулирование мощности электродвигателей или в аудио секторе для класса D усилителей . Импульсно-ступенчатая модуляция (PSM) — это метод, используемый для выходных каскадов передачи с амплитудной модуляцией большей мощности .
При импульсной кодовой модуляции (ИКМ) гребенка импульсов , периодическая последовательность коротких отдельных импульсов, умножается на входной сигнал, чтобы получить выходной сигнал («сигнал передачи»). Затем отдельные выходные значения квантуются, то есть преобразуются в конечное число уровней. Эта модуляция используется в некоторых аналого-цифровых преобразователях , особенно когда последовательность сигналов должна быть получена непрерывно, как в случае оцифровки голосовых и музыкальных сигналов.
Цифровая модуляция (манипуляция)
Тот самый вид модуляции, который используется для передачи данных в компьютерных сетях.
| Определение: |
| Цифровой модуляцией называется процесс преобразования битов в соответствующие аналоговые сигналы. |
Цифровую модуляцию принято называть манипуляцией, поэтому часто может встречаться именно этот термин.
Носителем так же, как и в случае аналоговой модуляции является колебание.
Основные методы цифровой модуляции
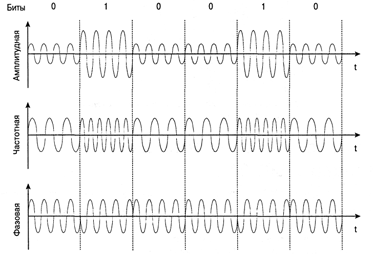
- Амплитудная
- Частотная
- Фазовая
- Квадратурная амплитудная (амплитудно-фазовая)
| Амплитудная (ASK — Amplitude Shift Keying) | Частотная (FSK — Frequency Shift Keying) | Фазовая (PSK — Phase Shift Keying) | Квадратурная амплитудная (QAM — Quadrature Amplitude Modulation) |
|---|---|---|---|
| Меняется амплитуда импульсов | Меняется частота импульсов | Меняется фаза колебания | Меняется одновременно и амплитуда, и фаза |
| Для передачи 1 используется большая амплитуда, для передачи 0 — малая, иногда нулю соответствует отсутствие колебания. | Для передачи 1 используется высокая частота колебаний, для передачи 0 — низкая. | Для передачи 1 используется сдвиг фазы на . | Для передачи 1 используется большая амплитуда и сдвиг фазы на . |
Многопозиционные методы
Для разных видов манипуляции существуют методы, позволяющие передавать не только 0 и 1 в рамках одного сигнала, такие методы получили название многопозиционные.
Суть этих методов в том, что один элемент линейного сигнала несет информацию о большем числе битов, чем в обычных двухпозиционных методах.
Работает это очень просто. Например, в многопозиционной амплитудной манипуляции зададим не 2 амплитуды, которые будут кодировать 0 или 1, а 4, которые будут соответствовать 00, 01, 10, 11 по мере увеличения амплитуды. Для многопозиционной частотной манипуляции используется больше частот, а для многопозиционной фазовой манипуляции, соответственно, больше сдвигов.
Да, это действительно позволяет повысить удельную скорость передачи информации, но при этом начинают возникать ошибки, связанные с погрешностью передачи.
Рассмотрим самые распространенные методы:
BPSK, QPSK, 8-PSK
| BPSK | QPSK | 8-PSK |
|---|---|---|
| Binary Phase Shift Keying является обычной бинарной фазовой манипуляцией, которую мы рассматривали выше в рамках основных методов, позволяет закодировать 1 бит информации за сигнал. Не является многопозиционным методом. | Quadrature Phase Shift Keying переводится как квадратурная фазовая манипуляция и представляет собой разделение на 4 фазы, которые позволяют закодировать 2 бита за сигнал. | 8 Phase Shift Keying представляет собой разделение на 8 фаз, которые позволяют закодировать 3 бита за сигнал. |
QAM-16, QAM-64
С простой квадратурной амплитудной манипуляцией мы уже знакомы, теперь посмотрим на 2 многопозиционные вариации. Напомню, что это комбинация амплитудной и фазовой манипуляций.
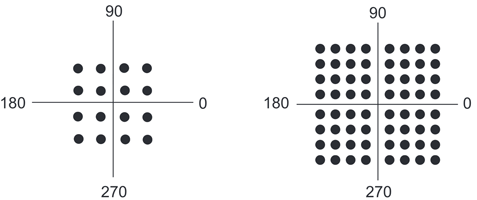
QAM-16 использует 16 комбинаций амплитудных и фазовых сдвигов, которые позволяют передавать 4 бита информации за 1 сигнал, а с помощью QAM-64, который использует 64 комбинации, можно передать целых 6 бит за сигнал.
Каждая комбинация задается углом, который соответствует фазе и расстоянием от начала координат, которое показывает величину амплитуды.
Ниже показана симуляция принципа работы квадратурной амплитудной манипуляции на примере QAM-16 и расположение точек для QAM-16 и QAM-64 соответственно.
4.2. Сигналы с непрерывной амплитудной модуляцией
Рассмотрение модулированных сигналов начнем с сигналов, у которых в качестве изменяемого параметра выступает амплитуда несущего колебания. Модулированный сигнал в этом случае является амплитудно-модулированным или сигналом с амплитудной модуляцией (АМ-сигналом).
Как уже было отмечено выше, основное внимание будет уделено сигналам, несущее колебание которых представляет собой гармоническое колебание вида
,
где – амплитуда несущего колебания,
– частота несущего колебания.
Здесь и далее полагается, что начальные фазы гармонических колебаний равны нулю.
В качестве модулирующих сигналов сначала рассмотрим непрерывные сигналы . Тогда модулированные сигналы будут являться сигналами с непрерывной амплитудной модуляцией. Такой сигнал описывается выражением
, (4.2)
где – огибающая АМ-сигнала,
– коэффициент амплитудной модуляции.
Из выражения (4.2) следует, что АМ-сигнал представляет собой произведение огибающей на гармоническую функцию . Коэффициент амплитудной модуляции характеризует глубину модуляции и в общем случае описывается выражением
. (4.3)
Очевидно, при сигнал представляет собой просто несущее колебание.
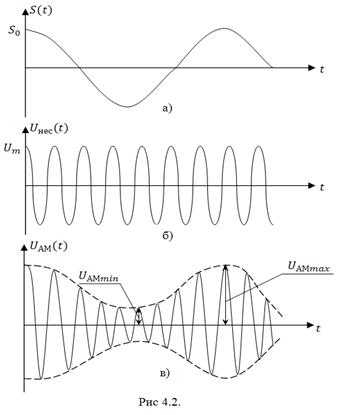
Для более детального анализа характеристик АМ-сигналов рассмотрим простейший АМ-сигнал, в котором в качестве модулирующего сигнала выступает гармоническое колебание
, (4.4)
где , – соответственно амплитуда и частота модулирующего (управляющего) сигнала, причем . В этом случае сигнал описывается выражением
, (4.5)
и называется сигналом однотональной амплитудной модуляции.
На рис. 4.2 изображены модулирующий сигнал , колебание несущей частоты и сигнал .
Для такого сигнала коэффициент глубины амплитудной модуляции равен
.
Воспользовавшись известным тригонометрическим соотношением
после несложных преобразований получим
(4.6)
Выражение (4.6) устанавливает спектральный состав однотонального АМ-сигнала. Первое слагаемое представляет собой немодулированное колебание (несущее колебание). Второе и третье слагаемые соответствуют новым гармоническим составляющим, появившимся в результате модуляции амплитуды несущего колебания; частоты этих колебаний и называются нижней и верхней боковыми частотами, а сами составляющие – нижней и верхней боковыми составляющими.
Амплитуды этих двух колебаний одинаковы и составляют величину
, ( 4.7)
На рис. 4.3 изображен амплитудный спектр однотонального АМ-сигнала. Из этого рисунка следует, что амплитуды боковых составляющих располагаются симметрично относительно амплитуды и начальной фазы несущего колебания. Очевидно, ширина спектра однотонального АМ-сигнала равна удвоенной частоте управляющего сигнала
.
В общем случае, когда управляющий сигнал характеризуется произвольным спектром, сосредоточенным в полосе частот от до , спектральный характер АМ-сигнала принципиально не отличается от однотонального.
На рис. 4.4 изображены спектры управляющего сигнала и сигнала с амплитудной модуляцией. В отличие от однотонального АМ-сигнала в спектре произвольного АМ-сигнала фигурируют нижняя и верхняя боковые полосы. При этом верхняя боковая полоса является копией спектра управляющего сигнала, сдвинутой по оси частот на
величину , а нижняя боковая полоса представляет собой зекальное отображение верхней. Очевидно, ширина спектра произвольного АМ-сигнала
, (4.8)
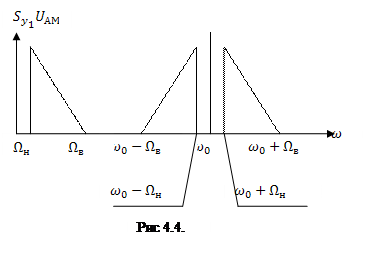
т.е. равна удвоенной верхней граничной частоте управляющего сигнала.
Возвратимся к сигналу однотональной амплитудной модуляции и найдем его энергетические характеристики. Средняя мощность АМ-сигнала за период управляющего сигнала определяется по формуле:
. (4.9)
Так как , а , положим , где . Подставляя выражение (4.6) в (4.9), после несложных, но достаточно громоздких преобразований с учетом того, что и с использованием тригонометрических соотношений
и 
,
получим
. (4.10)
Здесь первое слагаемое характеризует среднюю мощность несущего колебания, а второе – суммарную среднюю мощность боковых составляющих, т.е.
.
Так как суммарная средняя мощность боковых составляющих делится поровну между нижней и верхней, что вытекает из (4.7), то отсюда следует
. (4.11)
Таким образом, на передачу несущего колебания в АМ-сигнале тратится более половины мощности (с учетом того, что ), чем на передачу боковых составляющих. Так как информация заложена именно в боковых составляющих, передача составляющей несущего колебания нецелесообразна с энергетической точки зрения. Поиск более эффективных методов использования принципа амплитудной модуляции приводит к сигналам балансной и однополосной амплитудной модуляции.
В чем суть модуляции?
Возьмем высокочастотное колебание. Само по себе оно не несет никакой информации. Его мы будем использовать в качестве основного компонента передаваемого сигнала. Частоту этого колебания называют несущей.
Для того, чтобы начать передавать полезную информацию, нам нужно каким-нибудь образом видоизменить несущую частоту так, чтобы она повторяла закономерности сигнала, который мы хотим передать. Иными словами, нам нужно сделать так, чтобы она несла информацию о нашем полезном сигнале.
Это самое видоизменение называется модуляцией.
Модуляция осуществляется с помощью модулятора со стороны отправителя, а с помощью демодулятора на стороне получателя высокочастотный сигнал преобразуется обратно в низкочастотный. Они собраны в одно устройство под названием модем, которое получилось благодаря слиянию слов МОдулятор и ДЕМодулятор.
Есть разные принципы модуляции, некоторые из которых рассмотрим ниже.
Самым древним методом модуляции можно назвать прерывание несущей частоты, которое использовалось в телеграфах. Этот метод, конечно, нельзя назвать в полной мере модуляцией, но тем не менее о нем нельзя не упомянуть в данной теме.
Виды модуляции
Теперь рассмотрим более формальные определения.
| Определение: |
| Модуляцией называется процесс изменения одного или нескольких параметров высокочастотного несущего колебания по закону низкочастотного информационного сигнала. |
| Определение: |
| Модулирующий сигнал — сигнал, хранящий передаваемую информацию. |
| Определение: |
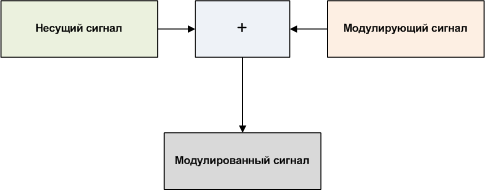
| Несущий сигнал — сигнал, выполняющий роль переносчика информации. |
| Определение: |
| Модулированный сигнал — сигнал, получающийся после посадки модулирующего сигнала на несущий сигнал. |
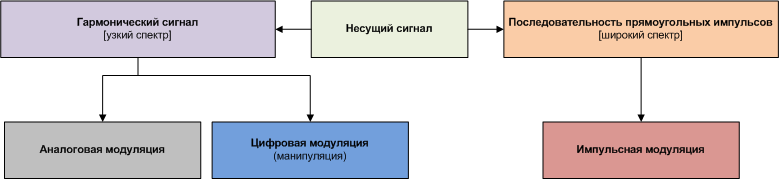
| Фиксированный уровень | Гармонический сигнал | Импульсы |
|---|---|---|
| Прямая модуляция | Аналоговая модуляция | Импульсная модуляция |
| Цифровая модуляция |
Цифровые модуляции
При цифровой модуляции параметры несущей, амплитуда или угол (аргумент) переключаются между несколькими дискретными значениями в соответствии с передаваемыми двоичными кодами.
Элементарные модуляции
- Модуляция » все или ничего» ( OOK (en) : On Off Keying ) с переменной длительностью — это то, что используется в телеграфии (азбука Морзе). По историческим причинам он также называется CW . Он особенно подходит для слухового распознавания оператором. В случае, когда эта модуляция осуществляется вручную, мы также говорим о манипуляции.
- При модуляции со сдвигом амплитуды ( ASK или амплитудная манипуляция ) амплитуда переключается между несколькими дискретными значениями.
- При частотной модуляции ( FSK или частотная манипуляция ) и при фазовой манипуляции ( PSK ) переключаются соответственно частота и фаза.
- В APK (или QAM) фаза и амплитуда принимают разные дискретные значения.
В зависимости от количества возможных уровней перед кодом будет добавлено число: таким образом, 8xPSK соответствует переключению между 8 значениями фазы, что позволяет передавать слова из 3 бит (8 значений) в каждый момент переключения.
Сложные модуляции
Более сложные комбинации используются для оптимизации пропускной способности по сравнению с полосой пропускания. Таким образом, сочетание двух амплитудной и фазовой модуляции одновременно на одной и той же несущей позволяет удвоить скорость передачи данных. Имена сложны и многочисленны, они объединены числом, определяющим количество возможных состояний и букв отдельных используемых модуляций. Например, 8x QPSK имеет 8 состояний (2 3 ) и позволяет передавать 3 одновременных бита путем модуляции двух несущих в квадратуре.
Для получения определенных преимуществ часто используются особые случаи: таким образом, MSK или минимальная манипуляция сдвигом — это цифровая частотная модуляция с точным индексом модуляции и минимальной спектральной шириной.
Если поднесущая модулируется, а затем модулируется несущая, имена становятся еще более сложными: Таким образом, AFSK — это частотная модуляция поднесущей. Модуляция AFSK-PM объединяет фазовую модуляцию несущей с помощью частотно-модулированной поднесущей.
Другой тип комплексной модуляции — OFDMA , используемый в последних поколениях мобильных сетей , который сочетает в себе частотное мультиплексирование (тысячи ортогональных поднесущих ), временное мультиплексирование и независимую модуляцию каждой поднесущей в QPSK или QAM .
Математика
В первой статье данной главы мы обсудили парадоксальную величину, называемую мгновенной частотой. Если вы считаете этот термин незнакомым или запутанным, вернитесь на эту страницу и прочитайте раздел «Частотная модуляция (ЧМ, англ. FM) и фазовая модуляция (ФМ, англ. PM)». Тем не менее, вы всё еще можете быть немного запутаны, и это понятно: идея мгновенной частоты нарушает основной принцип, согласно которому «частота» указывает, как часто сигнал завершает полный цикл: десять раз в секунду, миллион раз в секунду или сколько бы то ни было раз.
Мы не будем пытаться заниматься каким-либо тщательным или всесторонним рассмотрением мгновенной частоты в качестве математической концепции
(Если вы намерены подробно изучить эту проблему, вот академический документ, который должен помочь.) В контексте FM важно понять, что мгновенная частота естественно вытекает из того, что частота сигнала несущей изменяется непрерывно в ответ на модулирующую волну (т.е. низкочастотный сигнал)
Мгновенное значение модулирующего сигнала влияет на частоту в определенный момент, а не на частоту одного или нескольких полных циклов.
На самом деле это верно только для аналоговой частотной модуляции; в цифровой ЧМ один бит соответствует дискретному числу циклов. Это приводит к интересной ситуации, когда более старая технология (аналоговая ЧМ) менее интуитивно понятна, чем более новая технология (цифровая частотная модуляция, также называемая частотной манипуляцией или FSK (Frequency Shift Keying)).
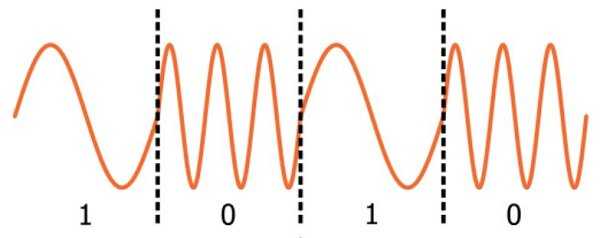Вам не нужно размышлять над мгновенной частотой, чтобы понимать цифровую частотную модуляцию
Как и в предыдущей статье мы будем обозначать несущую как sin(ωнесt). У нее уже есть частота (а именно, ωнес), поэтому мы должны использовать термин «дополнительное отклонение частоты» для обозначения частотной составляющей, внесенной процедурой модуляции. Этот термин несколько вводит в заблуждение, поскольку «дополнительное» подразумевает более высокую частоту, тогда как модуляция может приводить к несущей частоте, которая выше или ниже номинальной несущей частоты. Фактически поэтому частотная модуляция (в отличие от амплитудной модуляции) не требует смещенного низкочастотного сигнала: положительные значения низкочастотного сигнала увеличивают частоту несущей, а отрицательные значения низкочастотного сигнала уменьшают частоту несущей. В этих условиях демодуляция не является проблемой, поскольку все значения низкочастотного сигнала соответствуют уникальным частотам.
В любом случае, вернемся к нашему сигналу несущей: sin(ωнесt). Если мы добавим низкочастотный сигнал (xнч) к величине внутри круглых скобок, мы получим отклонение фазы, линейно пропорциональное низкочастотному сигналу. Но нам нужна частотная модуляция, а не фазовая, поэтому мы хотим, чтобы линейно пропорционально низкочастотному сигналу было отклонение частоты. Из первой статьи данной главы мы знаем, что мы можем получить частоту, взяв производную фазы по времени. Таким образом, если мы хотим, чтобы частота была пропорциональна xнч, мы должны добавить не сам низкочастотный сигнал, а скорее интеграл от низкочастотного сигнала (поскольку взятие производной отменяет интеграл, у нас остается xнч как отклонение частоты).
\
Единственное, что нам нужно здесь добавить, это индекс модуляции m. В предыдущей статье мы увидели, что индекс модуляции можно использовать для того, чтобы изменения амплитуды несущей были более или менее чувствительны к изменениям амплитуды низкочастотного сигнала. Его функция в FM аналогична: индекс модуляции позволяет нам точно настраивать интенсивность изменения частоты, которое возникает при изменении амплитуды низкочастотного сигнала.
\
сказка
Сами речь и музыка основаны на модуляции. Одно только движение языка и губ вызывает щелчки и шлепки, которые нельзя услышать далеко. Звук из гортани разносится намного дальше и уже служит младенцу носителем, через непрерывные (аналоговые) изменения громкости и высоты звука он сообщает о своем состоянии. Модуляция используется преднамеренно в .
Гульельмо Маркони осуществил первую радиопередачу через Ла-Манш в 1899 году, включив и выключив передатчик с поп-искрами . Код Морзе можно передавать с помощью этой цифровой модуляции . Когерер в приемнике ответил на высокочастотный сигнал и нестационарный выход передатчика был слышен как хрип. В то время избирательность не играла роли, так как количество каналов все еще было довольно ограниченным. В то время как Маркони стремился к более высокой мощности передачи, Реджинальд Фессенден в то же время улучшил чувствительность приемников.
До 1913 года передатчики можно было только включать и выключать, что в лучшем случае можно охарактеризовать как очень элементарную модуляцию. Для модуляции широким спектром сигналов, тонкие нюансы которых также необходимо передавать, требуется схема генератора, которая изначально генерирует постоянный сигнал — это стало возможным только после изобретения схемы Мейснера . Это было началом трансляции .
Вступление
Цель
Модуляция и демодуляция — это два этапа передачи информации между двумя пользователями. Например, чтобы заставить двух пользователей электронной почты общаться по телефонной линии, необходимы программное обеспечение, компьютер, протоколы , модулятор и демодулятор. Телефонная линия является каналом передачи, ее полоса пропускания сокращена, на нее влияют затухания и искажения. Модуляция преобразует двоичную информацию из протоколов и программного обеспечения в напряжение и ток в линии. Тип используемой модуляции должен быть адаптирован, с одной стороны, к сигналу (в данном случае цифровой), к требуемым характеристикам (коэффициенту ошибок) и характеристикам линии.
Таким образом, модуляция позволяет преобразовать спектр сообщения в частотную область, которая больше подходит для средств распространения, и обеспечить после демодуляции качество, требуемое другими уровнями системы.
Целью аналоговой модуляции является обеспечение достаточного качества передачи аналоговой информации (голоса, музыки, изображения) в пределах используемого канала и приложения.
Целью цифровых модуляций является обеспечение максимальной скорости двоичных данных с частотой ошибок, приемлемой для восходящих и нисходящих протоколов и корректоров. В стеке протоколов OSI (стандартная архитектура цифровых телекоммуникаций) модуляция является основным элементом физического уровня .
Модем представляет собой комбинированный модулятор и демодулятор сборки позволяет двунаправленную линию связи.
Примеры
Первой модуляцией было ограничение амплитуды по принципу «все или ничего», изобретенное Сэмюэлем Морсом для проводных телеграфных соединений, но, как и прямая передача голоса по телефонному проводу, это, строго говоря, не модуляции. провод — это просто изображение выхода микрофона или манипулятора.
С открытием радиоволн амплитудная модуляция несущей волны была первой системой, использованной либо в радиотелеграфии (CW), либо в радиотелефонии (AM). Первые телевизионные передачи также были в AM, затем дополнены методами уменьшения полосы (уменьшение боковой полосы), а затем добавлением поднесущей передачи цвета.
Радиопередачи диапазона «FM» используют частотную модуляцию для монофонического канала и поднесущую для передачи стереофонического звука и данных « RDS ».
Модемы в домашних или деловых сетях сочетают аналоговую и цифровую модуляцию поднесущей для передачи данных.
Системы модуляции
Когда несколько единиц информации или независимых сигналов проходят через один и тот же канал с использованием различных модуляций или поднесущих, мы говорим о «системе модуляции».
Таким образом, в телевидении звук передается посредством амплитудной модуляции первой несущей, изображение — посредством амплитудной модуляции с уменьшенной боковой полосой на основной несущей, а цветовой компонент — посредством частотной или фазовой модуляции. Тогда мы будем говорить о системе PAL , например
,
Мультиплексирование
Процесс модуляции может включать в себя мультиплексированные передачи через общую среду распространения, то есть одновременные передачи различных сообщений, имеющих непересекающиеся спектры во время распространения.
Одним из типов мультиплексирования является мультиплексирование с частотным разделением, процесс, в котором каждое сообщение модулирует высокочастотную несущую, и все несущие передаются одновременно через одну и ту же среду.
Примером мультиплексирования является передача аналогового спутникового телевидения: каждый канал частотно модулируется видеосигналом, который содержит как поднесущую системы цветности (PAL в Европе), так и мультиплексирование поднесущих различных Звуковые телепрограммы и радио.
Кодификация
В дальнейшем используются международные сокращения, используемые в стандартах и частотных агентствах. Существуют и указаны некоторые эквивалентные французские сокращения.
Угловая модуляция
Частотная и фазовая модуляции кодируют информацию во временны́х характеристиках передаваемого сигнала и, следовательно, устойчивы к амплитудному шуму и нелинейности усилителя. Частота сигнала не может быть изменена шумом или искажением. Могут быть добавлены дополнительные частотные составляющие, но исходная частота всё равно будет присутствовать. Разумеется, шум оказывает негативное влияние на FM и PM системы, но шум напрямую не искажает характеристики сигнала, которые использовались для кодирования низкочастотных данных.
Как упоминалось выше, разработка усилителя мощности включает в себя компромисс между эффективностью и линейностью. Угловая модуляция совместима с низколинейными усилителями, и эти низколинейные усилители более эффективны с точки зрения энергопотребления. Таким образом, угловая модуляция является хорошим выбором для маломощных радиочастотных систем.
Ширина полосы частот
Эффекты в частотной области от амплитудной модуляции более просты, чем от частотной и фазовой модуляций
Это можно считать преимуществом AM: важно иметь возможность прогнозировать ширину полосы частот, занимаемую модулированным сигналом
Однако сложность прогнозирования спектральных характеристик FM и PM актуальна больше для теоретической части проектирования. Если мы сосредоточимся на практических соображениях, угловая модуляция может считаться выгодной, поскольку она может преобразовывать заданную ширину полосы частот низкочастотного сигнала в несколько меньшую (по сравнению с AM) ширину полосы частот передаваемого сигнала.
3.5. Энергетический спектр модулированных сигналов
До сих пор мы рассматривали модуляцию несущего колебания детерминированным процессом u(t), который отображает определенное сообщение или отдельную его реализацию. Совокупность же возможных сообщений представляет собой некоторый случайный процесс. Так, при передаче речи или музыки статистические свойства передаваемых сообщений очень близки к свойствам нормального случайного процесса. Важнейшими характеристиками колебания, модулированного случайным процессом, являются функция корреляции и энергетический спектр.
Следует подчеркнуть, что модулированный сигнал является нестационарным случайным процессом даже тогда, когда модулирующие процессы (сообщения) стационарны. Энергетический спектр нестационарного случайного процесса определяется посредством двукратного усреднения — по множеству и по времени. Сначала определяется усредненная по времени корреляционная функция, а затем обратным преобразованием Фурье — искомый энергетический спектр.
Рассмотрим случай, когда передаваемое сообщение u(t) представляет собой стационарный процесс с u(t)=0, а переносчик — гармоническое колебание .
При амплитудной модуляции
s(t) = А0[1 + ти(t)]cos ωt,
где m — среднеквадратическое значение коэффициента модуляции. Функция корреляции модулированного сигнала
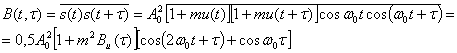
где Bu(t) — функция корреляции передаваемого сообщения u(t). Как видим, функция B(t, τ) зависит от времени, что указывает на нестационарность модулированного сигнала. После усреднения по времени получаем
(3.52)
Применяя к В (τ) преобразование Фурье (2.84), находим энергетический спектр сигнала при AM
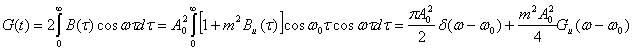
Таким образом, спектр модулированного по амплитуде гармонического колебания случайным процессом состоит из несущего колебания с частотой и смещенного на спектра передаваемого сообщения u(t).
Сигнал при угловой модуляции (ЧМ и ФМ) можно записать в общем виде
s(t) = А0cos ,
При ФМ , а при ЧМ.Здесь и — среднеквадратические значения девиации соответственно фазы и частоты.
Функция корреляции модулированного сигнала
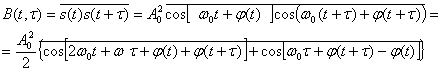
При усреднении по времени первое слагаемое обращается в нуль. Второе слагаемое не зависит от времени t поэтому
Обозначим разность и по известной формуле представим косинус суммы двух углов в виде
Средние по множеству значения косинуса и синуса можно найти, если известен закон распределения вероятностей сообщения u(t). Если u(t) подчиняется нормальному закону, то , являющееся линейным преобразованием от u(t), также будет иметь нормальное распределение с нулевым средним значением и дисперсией . Легко убедиться, что в этом случае:
Таким образом, усредненная по времени функция корреляции сигнала при угловой модуляции
(3.54)
Дисперсию процесса можно выразить через функцию корреляции или энергетический спектр сообщения u(t). Действительно.
(3.55)
где — функция корреляции процесса . При , поэтому ; при ЧМ , где , поэтому . Далее можно определить энергетический спектр модулированного сигнала путем преобразования Фурье (2.81) от функции (3.54).
3.6. Модуляция шумовой несущей
В качестве переносчика можно использовать не только периодические колебания, но и узкополосный случайный процесс. Такие переносчики также находят практическое применение. Например, в оптических системах связи, в которых используется некогерентное излучение, сигнал, по существу, представляет собой узкополосный гауссов шум.
Согласно (2.36) узкополосный случайный процесс можно представить как квазигармоническое колебание
с медленно изменяющимися огибающей и фазой . При амплитудной модуляции в соответствии с передаваемым сообщением изменяется огибающая U(t), при фазовой модуляции — фаза и при частотной — мгновенная частота .
Рассмотрим амплитудную модуляцию шумовой несущей. Выражение для модулированной несущей в этом случае можно записать в виде
y(t) = [1 + ти(t)]f(t),(3.57)
где f(t) — переносчик, u(t) — модулирующая функция (видеосигнал), m — коэффициент модуляции.
Предполагается, что модулирующий процесс u(t) также представляет собой стационарный нормальный процесс со средним значением, равным нулю u(t) = 0. Процессы f(t) и u(t) независимы. При этих ограничениях функция корреляции модулированной по амплитуде шумовой несущей будет
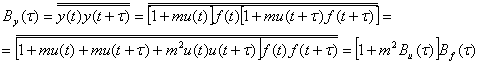(3.58)
Теперь находим энергетический спектр
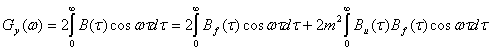
Первый интеграл дает энергетический спектр шумовой несущей . Для второго интеграла на основании теоремы о спектре произведения имеем
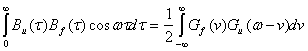
Окончательно спектр модулированной несущей будет равен:
(3.59)
Таким образом, спектр модулированной по амплитуде шумовой несущей получается суперпозицией спектра несущей и свертки этого спектра со спектром передаваемого сообщения, сдвинутого в область высоких частот на величину .Аналогично определяются функция корреляции и энергетический спектр при ФМ и ЧМ.
Применение «шумовых» сигналов позволяет ослабить влияние замираний в каналах с многолучевым распространением радиоволн. Поясним это на простейшем примере. Пусть на вход приемника поступают сигналы двух лучей и сдвигом на τ. время т. Мощность результирующего сигнала, определяемая за достаточно большое время Т,
где — функция корреляции сигнала, Р0— его средняя мощность. Функция корреляции шума быстро убывает с увеличением т и тем быстрее, чем шире его спектр. Следовательно, при достаточно большой ширине спектра можно считать 0 и , т. е. средняя мощность принятого сигнала, несмотря на замирания, остается примерно постоянной.